聊聊知乎订单系统迁移

本文主要介绍知乎订单系统后端语言栈的转型升级过程,包括其间踩过的一些坑和遇到的一些问题。一来是想通过本篇文章为其它应用服务转型提供借鉴经验,二来是总结对于订单系统的理解。鉴于文字功底不足,对于业务理解不充分的地方,欢迎留言交流。文章大纲如下:
- 迁移背景
- 前期准备
- 迁移方案
- 接口验证
- 指标梳理
- 可用性保障
- MTTR 快速响应
- MTBF 降低故障率
- 一致性保障
- 事后总结
- 目标回顾
- 执行计划
- 执行结果
- 问题整理
- 业务沉淀
- 方法论实践
- 参考文章
- 招聘信息
迁移背景
随着知乎整体技术栈的变化,原有的 Python 技术栈逐渐被抛弃,新的 Go 和 Java 技术栈逐渐兴起。知乎交易系统的稳定性相比其它业务系统的稳定性重要很多,因为交易系统核心链路发生故障不仅会造成数据问题,还会造成严重的资损问题。
随着公司业务的不断壮大发展,交易场景变得复杂,重构和优化难以避免,因为语言特性,Python 虽然开始撸代码很爽,但是后期的维护成本慢慢变高,不过 Python 在数据分析和人工智能方向上还是有很大优势的,只是在交易领域目前看起来不太合适。从技术生态上来说,用 Java 做交易系统会更有优势,所以接下来要说的知乎订单系统语言栈转型。
另外一个因素是 Python 的 GIL 锁导致它无法发挥多核的优势,性能上受到很大限制,在实际情况中遇到过多次主线程被 hang 住导致的可用性故障,所以坚定决心来迁移掉旧系统。
前期准备
工欲善其事,必先利其器。
语言栈转型首先要明确转型的三个开发流程,即 MRO (Migration, Reconstruction, Optimization)
- 迁移 就是把原语言代码照着抄一遍到新语言项目上,按照新语言的工程实现风格来做就可以。其间最忌掺杂代码优化和 bug 修复,会容易引起新的问题,增加验证代码的难度。
- 重构 目的是提高项目代码的可维护性和可迭代性,让代码更优雅和易读懂,可以放到迁移完成来做。
- 优化 通过在模块依赖、调用关系、接口字段等方面的调整来降低项目的复杂性,提高合理性。
对于语言栈转型来说,迁移流程是肯定要做的,重构和优化如何选择,可以按模块划分功能拆成子任务来分别评估方案,参考依据为现有模块如果同时优化或重构带来的直接收益和间接收益有多少。
- 收益:完成新旧语言栈的转换,系统维护性更好,模块边界更清晰。
- 成本:需要投入的人力成本,迁移过程中的并行开发成本,使有更高价值的工作被阻塞的损失。
- 风险:引入新的 bug,增加测试的复杂性。
在风险可控的前提下,成本与收益要互相权衡,一般会有两种方案可供参考:第一种是锁定需求,堆人力开发上线,一步到位;第二种则是小步快走,迭代上线,分批交付。
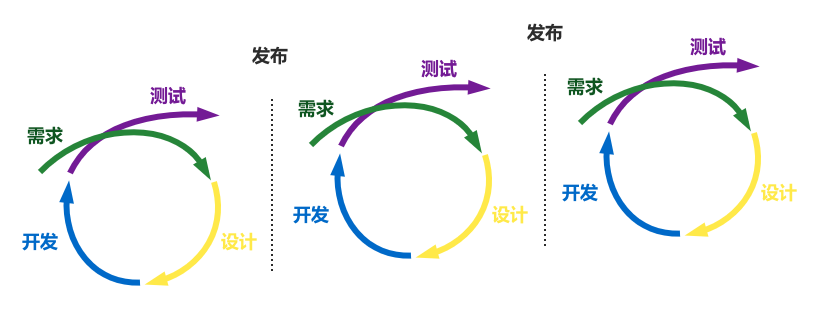
基于以上分析,在本次转型过程中,人力成本是一个更重要的因素,所以采用只迁移的方案,来压缩人力成本,降低 bug 引入风险的同时也具有很好的可测试性。并且为了不阻塞业务需求,采用小步快走的方式分批交付,以最长两周作为一个迭代周期进行交付。
迁移方案
确定了交付方式,下面我们需要梳理当前系统中的功能模块,做好任务拆分和排期计划。知乎交易系统在迁移前的业务是针对虚拟商品的交易场景,交易路径比较短,用户从购买到消费内容的流程如下:
- 在商品详情页浏览
- 生成订单进入收银台和用户支付
- 确认支付后订单交付
- 用户回到详情页消费内容
- 特定商品的七天无理由退款
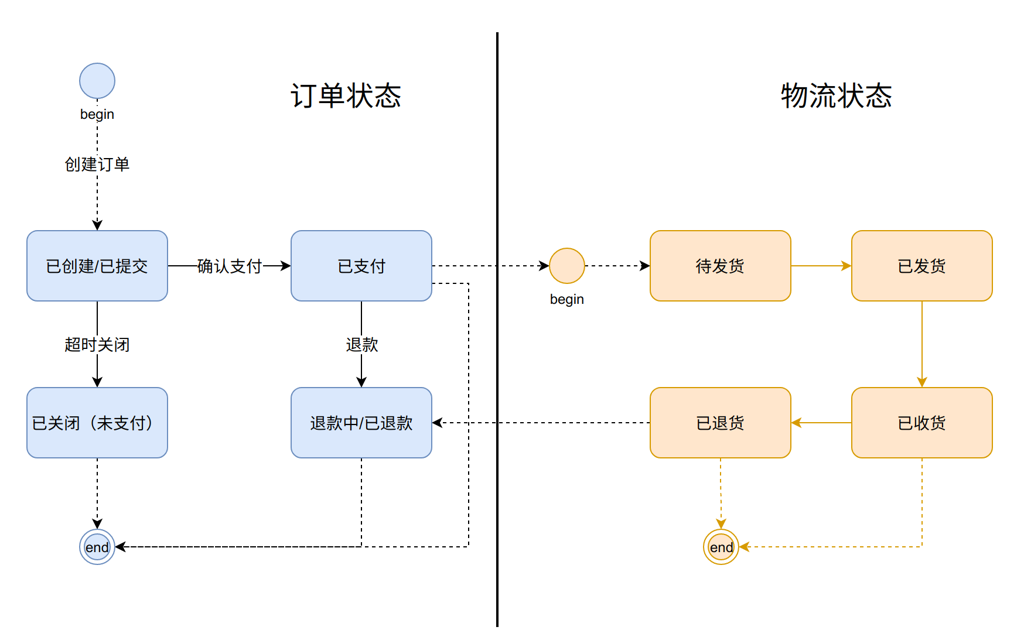
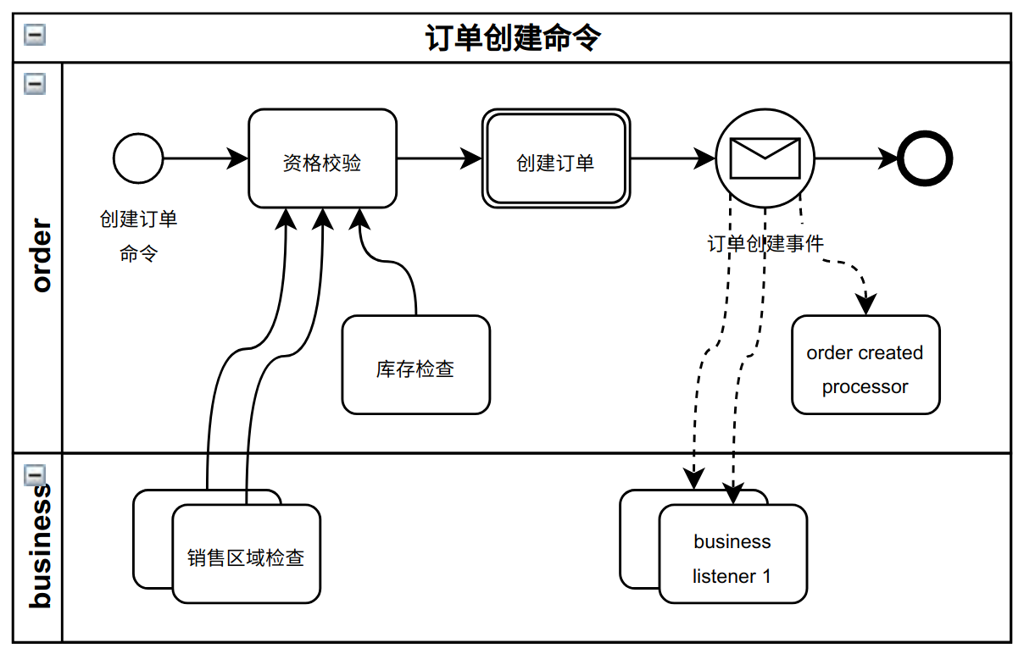
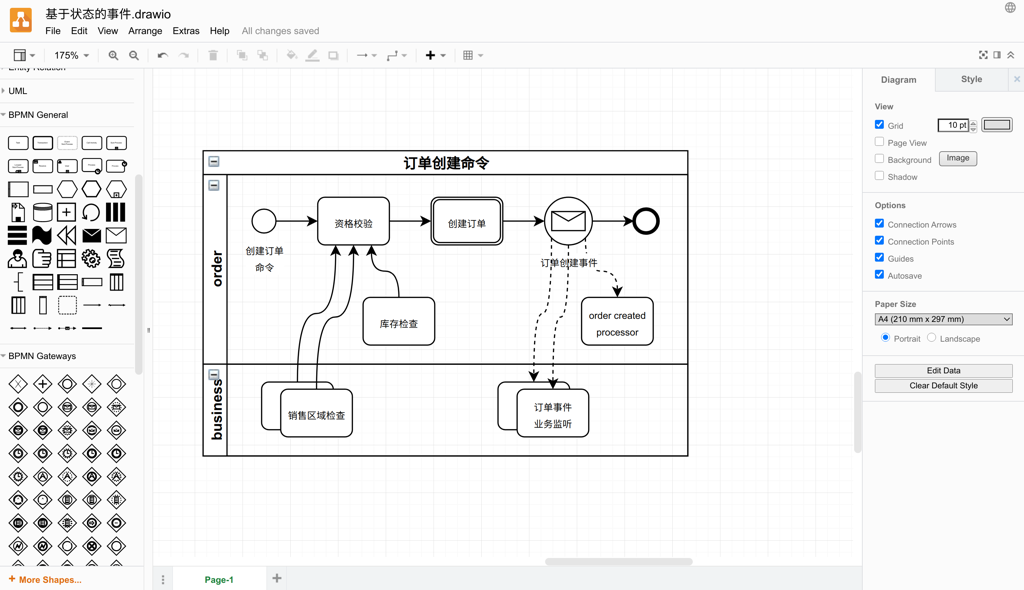
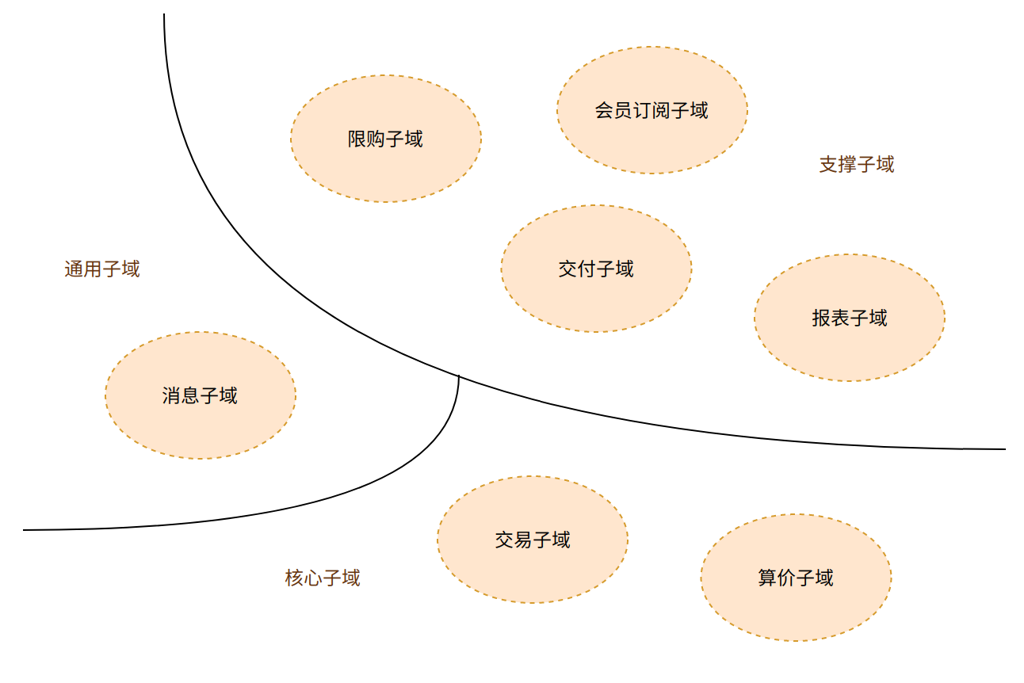
当时订单系统支持的功能还不多,业务模型和订单模型没有足够地抽象,梳理订单系统业务如下:
完成了订单模块的拆分后,新老系统如何无缝切换?如何做到业务无感?如何保障交易系统稳定性?出现故障如何及时止损?基于上面讲述的原则,将整个系统的迁移划分成两个阶段,迁移前后的数据存储和模型都不变。

接口验证
不论是在迁移的哪个阶段,总需要调整订单接口,可以从订单操作角度分为读操作和写操作,需要针对读接口和写接口做不同的验证方案。
写操作可以通过白名单测试以及灰度放量的方式进行验证上线,将接口未预期异常输出到 IM 工具以得到及时响应。主要的写操作相关接口有:
- 订单的创建接口。
- 订单绑定支付单的提交接口。
- 用户支付后回调确认接口。
- 用户发起退款接口。
下图展示的是 AB 平台的流量配置界面:
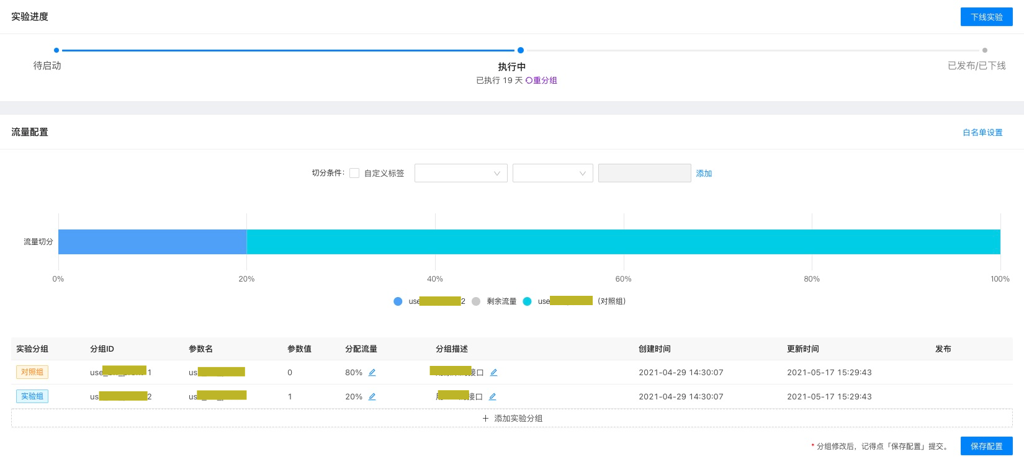
下图展示了部分交易预警通知消息:

读操作往往伴随在写操作中。我们利用平台的录制回放功能进行接口的一致性检查,通过对比得出差异排查问题。主要的读操作接口有:
- 获取支付方式列表接口
- 获取订单支付履约状态接口
- 获取充值列表接口
- 批量查询用户新客状态接口
下图展示的是流量录制回放系统的数据大盘:
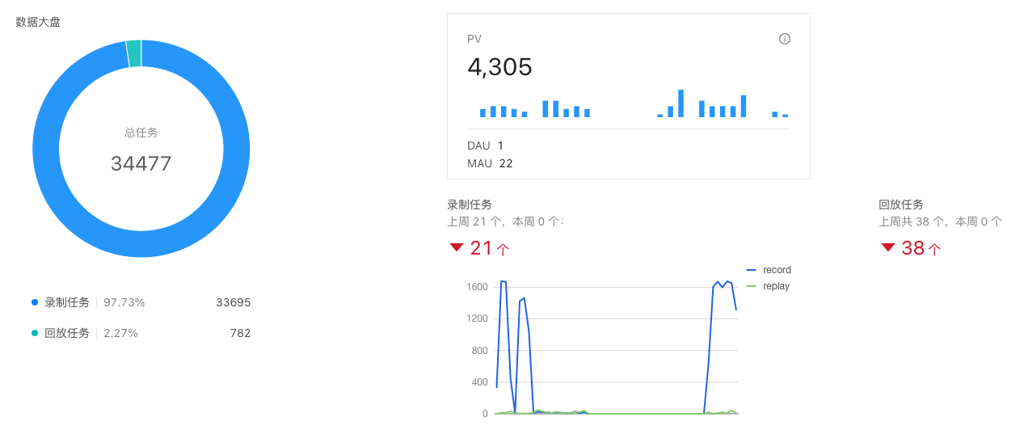
指标梳理
监控是我们系统的『第三只眼』,可以及时反应系统的健康状况,及时发出告警信息,并帮助我们在出现故障时分析问题和快速缩小排查范围。硬件、数据库、中间件的监控已经在平台层得到支持,这里只需要梳理出应用的监控指标。
- 日志监控:请求日志、服务端的错误日志。
- 订单业务指标
- 下单量、成单量、掉单量
- 单量环比数据
- 首次履约异常量
- 补偿机制履约量
- 各通知事件 P95 耗时
- 成功履约 P95 耗时
- 履约准时率/成功率
- 下单量、成单量、掉单量
- 支付业务指标
- 支付渠道履约延迟 P95
- 支付履约延迟 P95。
- 用户购买完整耗时 P95。
可用性保障
在整个交付的过程中,转型前后对 SLA 要提供一致的可用性保障,可以看看下面的几个衡量标准:
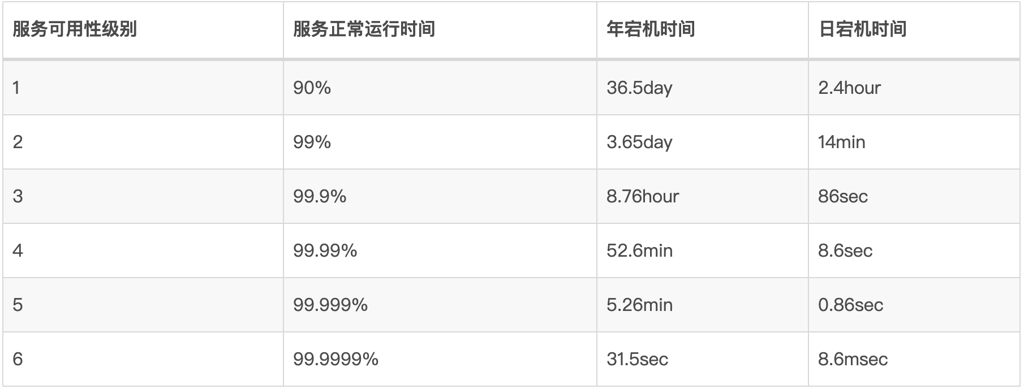
一般 3 个 9 的可用性全年宕机时间约为 8.76 小时,不同系统不同用户规模对于系统可用性的要求不一样,边缘业务的要求可能会低一些,但是对于核心链路场景 TPS 可能不高,但是必须要求保证高可用级别。如何保证或者提升服务的 SLA 是我们接下来要探讨的内容,一般有下面两个影响因素:
MTBF (Mean Time Between Failures) 系统服务平均故障时间间隔
MTTR (Mean Time To Recover) 系统服务平均故障恢复时长
也就是说我们要尽可能地降低故障频率,并确保出现故障后可以快速恢复。基于这两点我们在做系统平稳过渡时,要充分测试所有 case ,并且进行灰度方案和流量录制回放,发现异常立即回滚,定位问题解决后再重新灰度。
MTTR 快速响应
持续监控
感知系统稳定性的第一步就是监控,通过监控来反映系统的健康状况以及辅助定位问题,监控有两个方向:
第一个方向是指标型监控,这里监控是在系统代码中安排各种实时打点,上报数据后通过配置报表呈现出来的。
- 基础设施提供的机器监控以及接口粒度的响应稳定性监控。
- 物理资源监控,如 CPU、硬盘、内存、网络 IO 等。
- 中间件监控,消息队列、缓存、Nginx 等。
- 服务接口,HTTP、RPC 接口等。
- 数据库监控,连接数、QPS、TPS、缓存命中率、主从延迟等。
- 业务数据层面的多维度监控,从客户端和服务端两个角度来划分。
- 从客户端角度来监控服务端的接口成功率,支付成功率等维度。
- 从服务端角度从单量突变、环比变化、交易各阶段耗时等维度持续监控。
以上两点基于公司的 statsd 组件进行业务打点,通过配置 Grafana 监控大盘实时展示系统的健康状况。
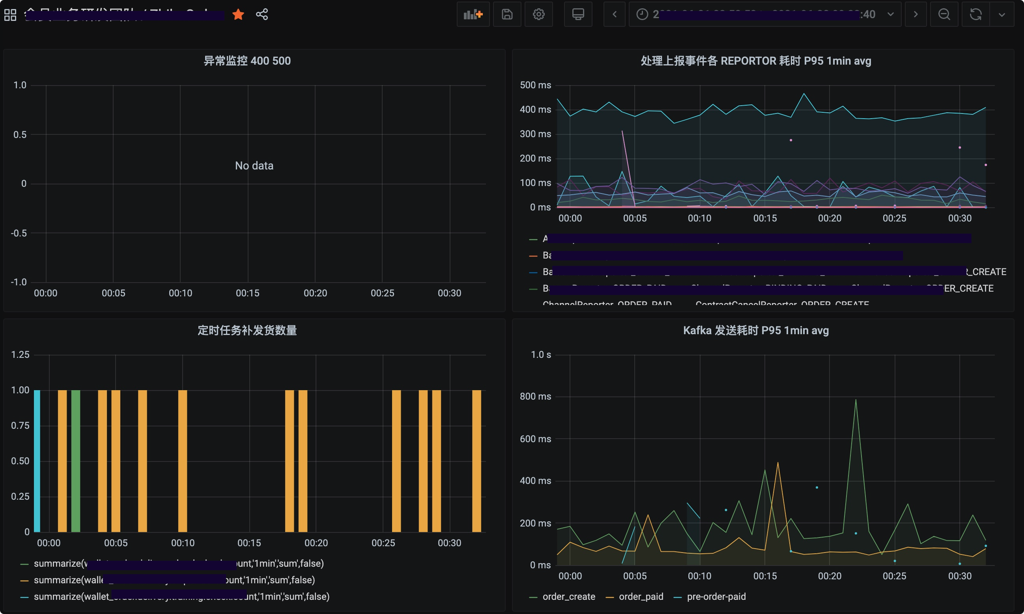
第二个方向是日志型监控,这主要依赖公司的 ELK 日志分析平台和 Sentry 异常捕获平台。通过 Sentry 平台可以及时发现系统告警日志和新发生的异常,便于快速定位异常代码的发生位置。ELK 平台则可以将关键的日志详细记录下来以便于分析产生的场景和复现问题,用来辅助修复问题。
异常告警
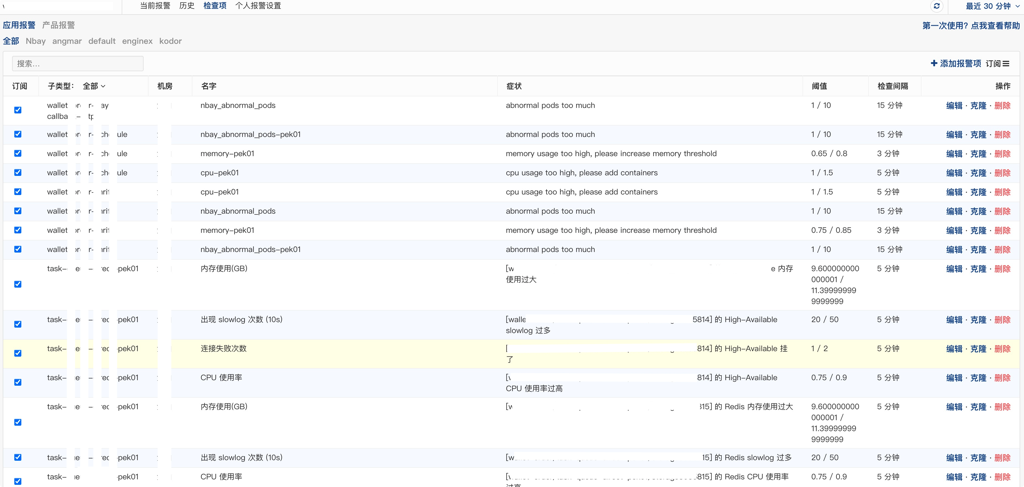
基于以上实时监控数据配置异常告警指标,能够提前预知故障风险,并及时发出告警信息。然而达到什么阈值需要告警?对应的故障等级是多少呢?
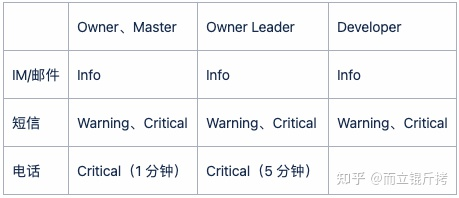
首先我们要在交易的黄金链路上制定比较严格的告警指标,从下单、提单、确认支付到履约发货的每个环节做好配置,配置的严重程度依次递增分为 Info、Warning、Critical。按照人员类别和通知手段来举例说明告警渠道:
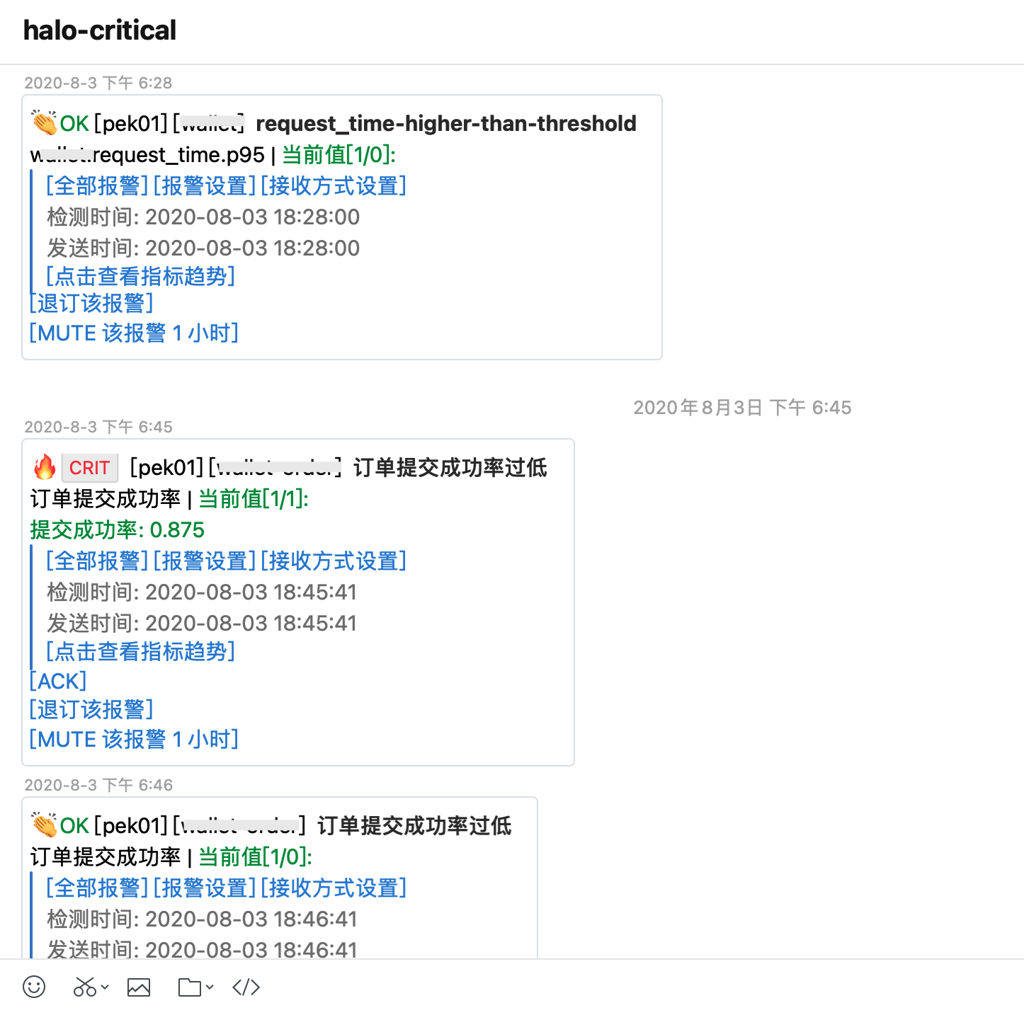
IM 中的预警消息截图如下:
订单主要预警点如下:
- 核心接口异常
- 掉单率、成单率突变
- 交易各阶段耗时增加
- 用户支付后履约耗时增加
- 下单成功率过低
MTBF 降低故障率
系统监控告警以及日志系统可以帮我们快速的发现和定位问题,以及时止损。接下来说的质量提升则可以帮助我们降低故障发生率以避免损失,主要从两个方向来说明:
规范化的验收方案
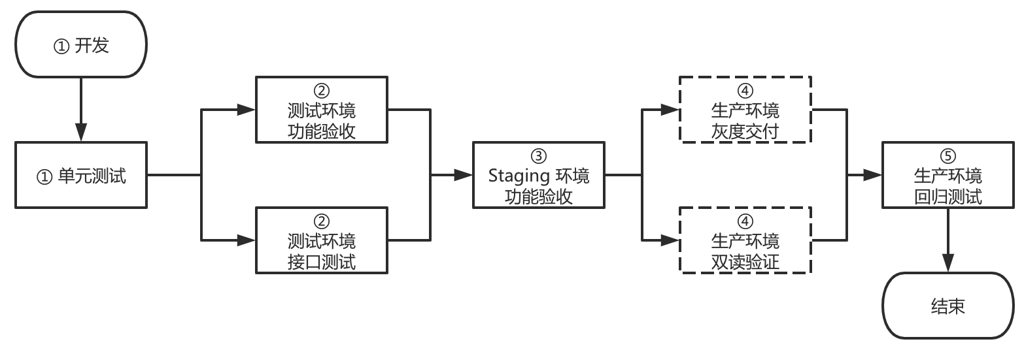
① 开发完成包括逻辑功能和单元测试,优先保证单测行数覆盖率再去保证分支覆盖率。然后在联调测试环境中自测,通过后向 QA 同学提测。
② QA 同学可以在测试环境下同时进行功能验收和接口测试,测试通过后便部署到 Staging 环境。
③ 在 Staging 环境下进行功能验收并通过。
④ 灰度交付以及双读验证可以根据实际情况选择性使用。
⑤ 上线后需要最后进行回归测试。
统一的编码规约以及多轮 CR 保障
代码上线前一般至少要经过两次代码评审,太小的 MR 直接拉一位同事在工位 CR 即可,超过百行的变更需要拉会研讨,两次评审的关注点也不同。
第一次评审应关注编码风格,这样可以避免一些因在写法上自由发挥而带来的坑,以此来沉淀出组内相对统一的编码规约,在编码的稳定性上建立基本的共识,提升代码质量。
第二次评审应关注代码逻辑,这里有个需要注意的点是,如果明确只做迁移,那么其间发现旧逻辑难理解的地方不要随便优化,因为在不了解背景的情况下很有可能会写一个 bug 带上线(这种事见过好几次)。另外这样也好去对比验证,验证通过上线后再去优化。
只有通过明确目的和流程并且遵循这个流程做,才能更快更好地交付有质量的代码。
一致性保障
每一个微服务都有自己的数据库,微服务内部的数据一致性由数据库事务来保障,Java 中采用 Spring 的 @Transtaction 注解可以很方便地实现。
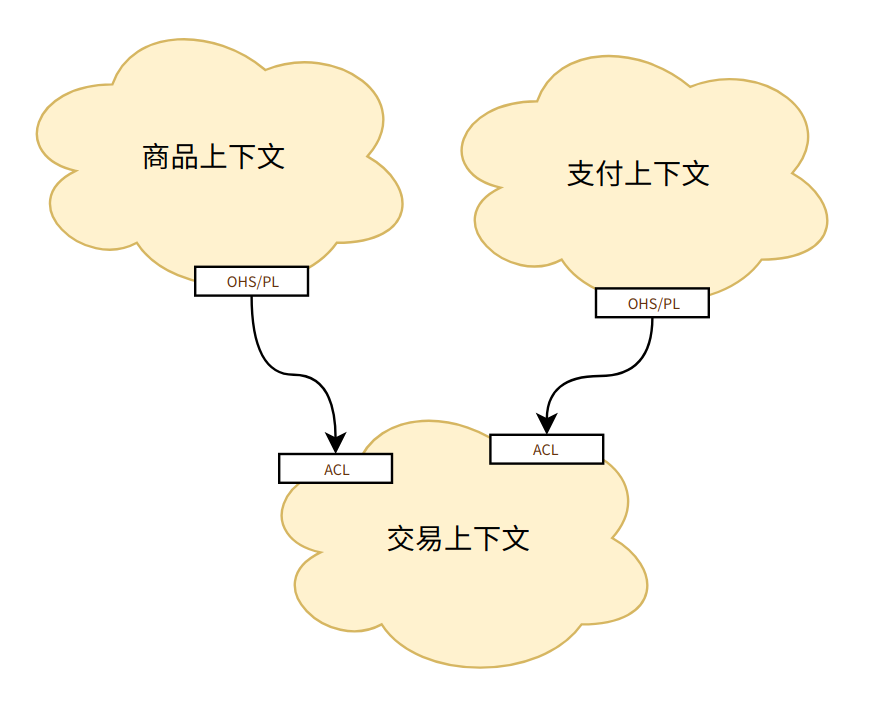
而跨微服务的分布式事务,像 支付、订单、会员三个微服务之间采用最终一致性,类似 TCC 模式的两阶段提交,订单通过全局发号器生成订单 ID,然后基于订单 ID 创建支付单,如果用户支付后订单会变更自身状态后通知会员微服务,履约成功则事务结束,履约失败则触发退款,如果用户未支付,那么订单系统将该订单以及支付单做关单处理。
对应一致性保障,我们对订单接口做了两个方面的处理:
分布式锁
对于上游的支付消息监听、支付 HTTP 回调、订单主动查询支付结果三个同步机制分别基于订单 ID 加锁后再处理,保证同步机制不会被并发处理。
接口幂等
加锁后对订单状态做了检查,处理过则响应成功,否则处理后响应成功,保证上游消息不会被重复处理。
订单对于下游的履约,是通过订单 ID 作为幂等 key 来实现的,以保证同一个订单不会被重复履约,并且通过 ACK 机制保证履约后不会再重复调到下游。
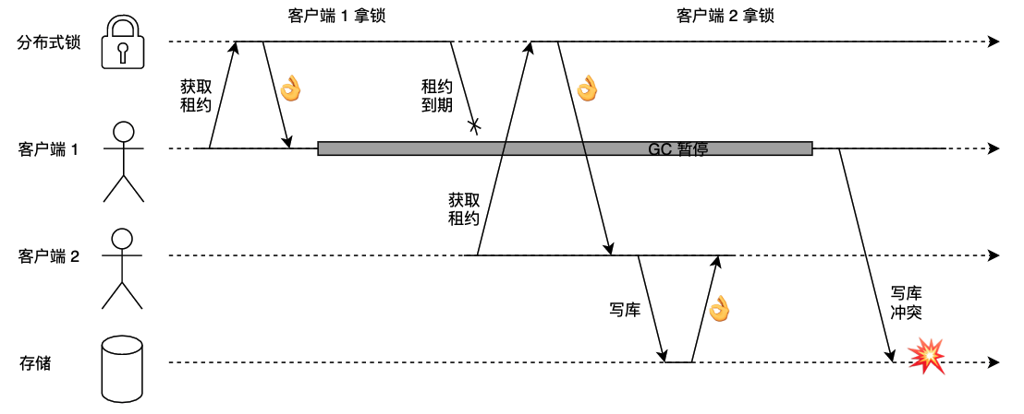
其中分布式锁采用 etcd 锁,通过锁租约续期机制以及数据库唯一索引来进一步保障数据的一致性。
补偿模式,虽然我们通过多种手段来保证了系统最终一致,但是分布式环境下会有诸多的因素,如网络抖动、磁盘 IO、数据库异常等都可能导致我们的处理中断。这时我们有两种补偿机制来恢复我们的处理:
带惩罚机制的延时重试
如果通知中断,或者未收到下游的 ACK 响应,则可以将任务放到延迟队列进行有限次的重试,重试间隔逐次递增。最后一次处理失败报警人工处理。
定时任务兜底
为了防止以上机制都失效,我们的兜底方案是定时扫描异常中断的订单再进行处理。如果处理依然失败则报警人工处理。
事后总结
目标回顾
目标一:统一技术栈,降低项目维护成本。目标结果是下线旧订单系统。
目标二:简化下单流程,降低端接入成本。目标结果是后端统一接口,端上整合 SDK。
执行计划
迁移的执行总共分成了三个大阶段:
第一阶段是迁移逻辑,即将客户端发起的 HTTP 请求转发到 RPC 接口,再由新系统执行。第一阶段做到所有的新功能需求都在新系统上开发,旧系统只需要日常维护。
第二阶段是通过和客户端同学合作,迁移并整合当前知乎所有下单场景,提供统一的下单购买接口,同时客户端也统一提供交易 SDK,新组件相对更加稳定和可监控,在经过灰度放量后于去年底完全上线。第二阶段做到了接口层的统一,更利于系统的维护和稳定,随着新版的发布,旧接口流量已经变得很低,大大降低了下阶段迁移的风险。
第三阶段是旧 HTTP 接口迁移,由新系统承载所有端的请求,提供相同规格的 HTTP 接口,最后通过修改 NGINX 配置完成接口迁移。第三阶段迁移完成后旧系统最终实现了下线。
执行结果
截至此文撰写时间,语言栈已经 100% 迁移到新的系统上,旧系统已经完全下线,总计下线 12 个系统服务, 32 个对外 HTTP 接口,21 个 RPC 接口,15 个后台 HTTP 接口。
根据 halo 指标,迁移前后接口 P95 耗时平均减少约 40%,硬件资源消耗减少约 20%。根据压测结果比较,迁移后支撑的业务容量增长约 10 倍。
系统迁移完成只是取得了阶段性的胜利,接下来系统还需要经过一些小手术来消除病灶,主要是以下几点:
- 不断细化监控粒度,优化告警配置,继续提高服务的稳定性。
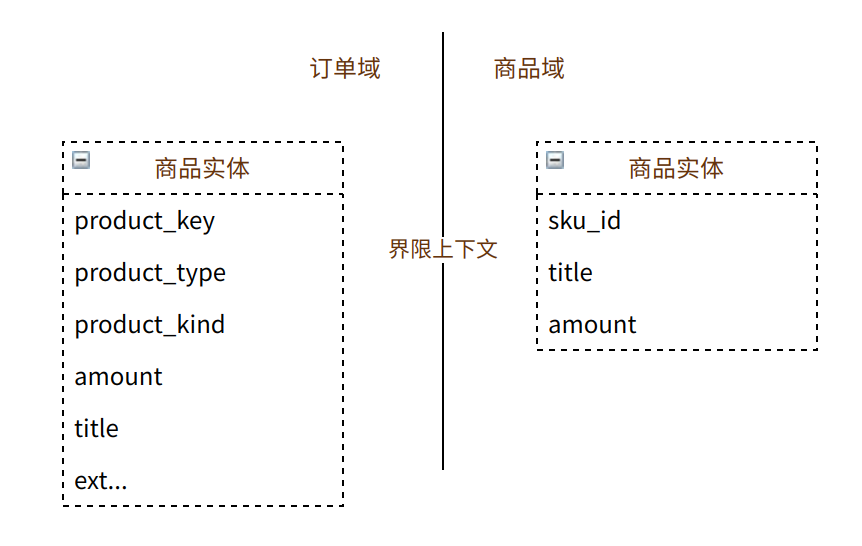
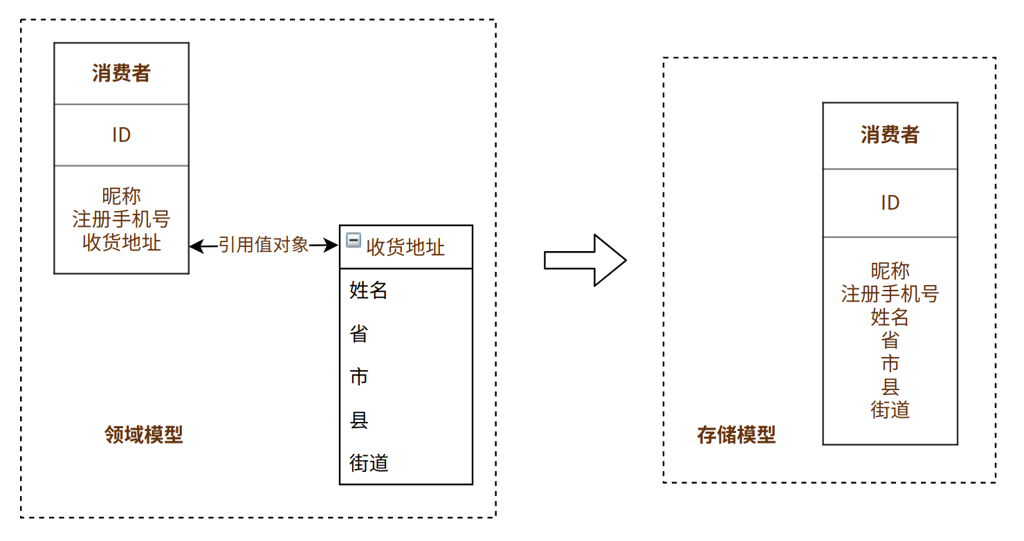
- 对于 Python 的硬翻译还需要不断重构和优化,这里借鉴 DDD 设计思想。
- 完善监控大盘,通过数据驱动来运营优化我们的流程。
- 项目复盘总结以及业务普及宣讲,提升人员对于业务细节的认知。
问题整理
迁移总是不能一帆风顺的,其间遇到了很多奇奇怪怪的问题,为此头发是真没少掉。
问题 1:迁移了一半新需求来了,又没有人力补上来怎么办?
迁移后再做重构和优化过程,其实很大一部分考量是因为人力不足啊,而且现状也不允许锁定需求。那么只能写两遍了,优先支持需求,后面再迁移。如果人力充足可以选择一个小组维护新的系统一个小组维护旧的系统。
问题 2:我明明请求了,可日志怎么就是不出来呢?
不要怀疑平台的问题,要先从自身找问题。总结两个原因吧,一个是新旧系统的迁移点太分散导致灰度不好控制,另一个是灰度开关忘记操作了,导致流量没有成功导到新系统上。这里要注意一个点就是在迁移过程中要尽可能的快速交付上线。
问题 3:公司 Java 基础服务不够完善,很多基础平台没有支持怎么办?
于是自研了分布式延迟队列、分布式定时任务等组件,这里就不展开聊了。
问题 4:如何保证迁移过程中两个系统数据的一致性?
首先我们前面讲到的是系统代码迁移,而数据存储不变,也就是说两个系统处理的数据会存在竞争,解决的办法是在处理时加上分布式锁,同时接口的处理也是要幂等的。这样即使在上下游系统做数据同步的时候也能避免竞争,保证数据的一致性。
就用户支付后支付结果同步到订单系统这一机制来说,采用推拉的机制。
① 用户支付后订单主动轮询支付结果,则是在主动拉取数据。
② 支付系统发出 MQ 消息被订单系统监听到,这是被动推送。
③ 支付成功后触发的订单系统 HTTP 回调机制,这也是被动推送。
以上三种机制结合使用使得我们系统数据一致性有一个比较高的保障。我们要知道,一个系统绝非 100% 可靠,作为交易支付的核心链路,需要有多条机制保证数据的一致性。
问题 5:用户支付后没有收到会员权益是怎么回事?
在交易过程中,订单、支付、会员是三个独立的服务,如果订单丢失了支付的消息或者会员丢失了订单的消息都会导致用户收不到会员权益。上一个问题中已经讲到最终一致性同步机制,可能因为中间件或者网络故障导致消息无法同步,这时可以再增加一个补偿机制,通过定时任务扫描未完成的订单,主动检查支付状态后去会员业务履约,这是兜底策略,可保障数据的最终一致。
业务沉淀
从接收项目到现在也是对订单系统从懵懂到逐渐加深理解的一个过程,对于当前交易的业务和业务架构也有了一个理解。
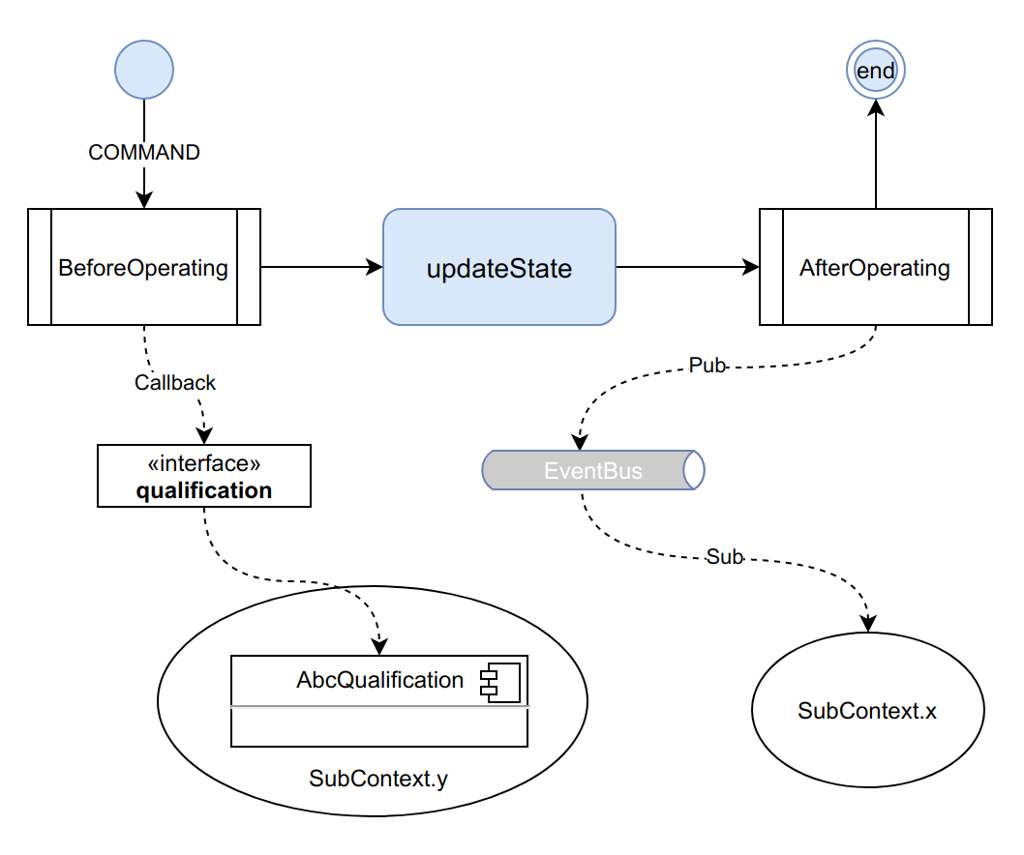
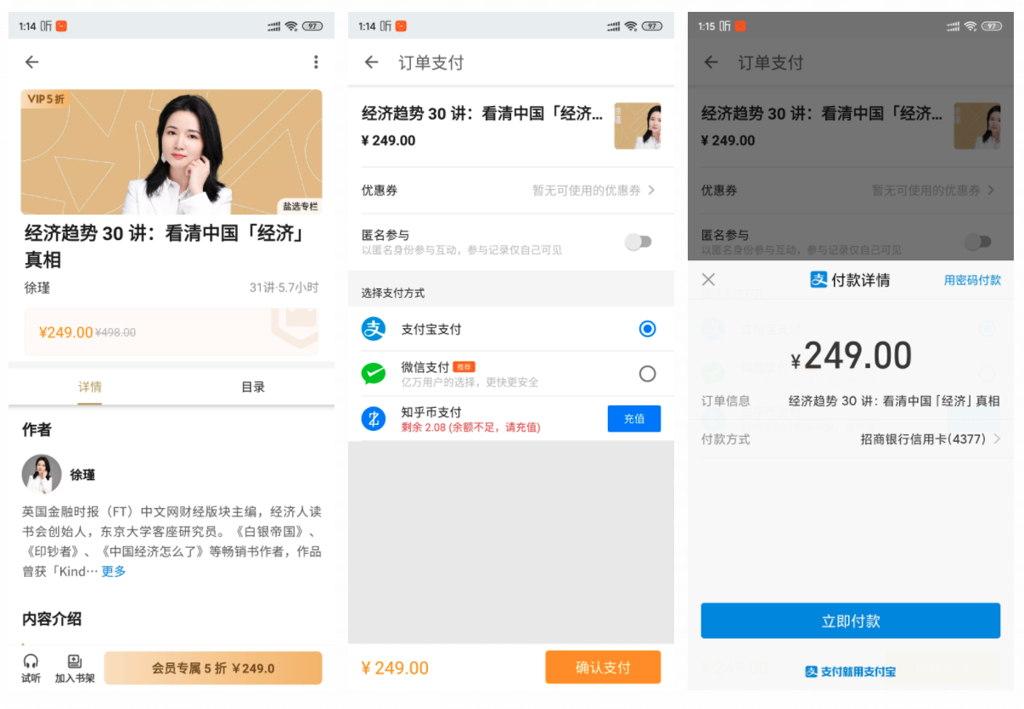
交易系统本身作为支付系统的上层系统,提供商品管理能力、交易收单能力、履约核销能力。外围业务子系统主要关注业务内容资源的管理。业务的收单履约管理接入交易系统即可,可减轻业务的开发复杂度。收单流程展示如下:
- 业务定制商品详情页,然后通过详情页底栏调用端能力进入订单收银台。在这里客户端需要调用业务后端接口来获取商品详情,然后调用交易底栏的展示接口获取底部按钮的情况。
- 用户通过底部按钮进入收银台后,在收银台可以选择支付方式和优惠券,点击确认支付调起微信或者支付宝付款。收银台展示以及获取支付参数的接口由交易系统提供。
- 订单后台确认收款后会通知业务履约,用户端会回到详情页,用户在详情页进入内容播放页享受权益。履约核销流程是业务后端与交易系统后端的接口调用来完成的。
现在知乎站内主要是虚拟商品的交易,一个通用的交易流程如下图:
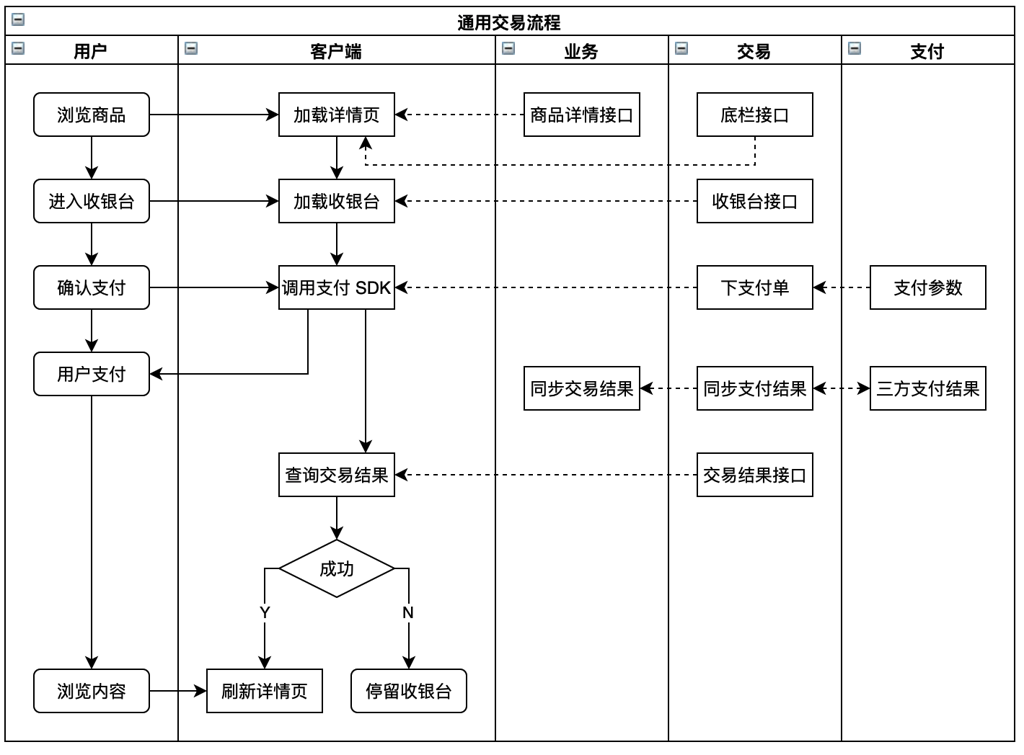
用户经历了从商品的浏览到进入收银台下单支付,再回到内容页消费内容。随着业务的发展,不同的交易场景和交易流程叠加,系统开始变得复杂,一个交易的业务架构慢慢呈现。
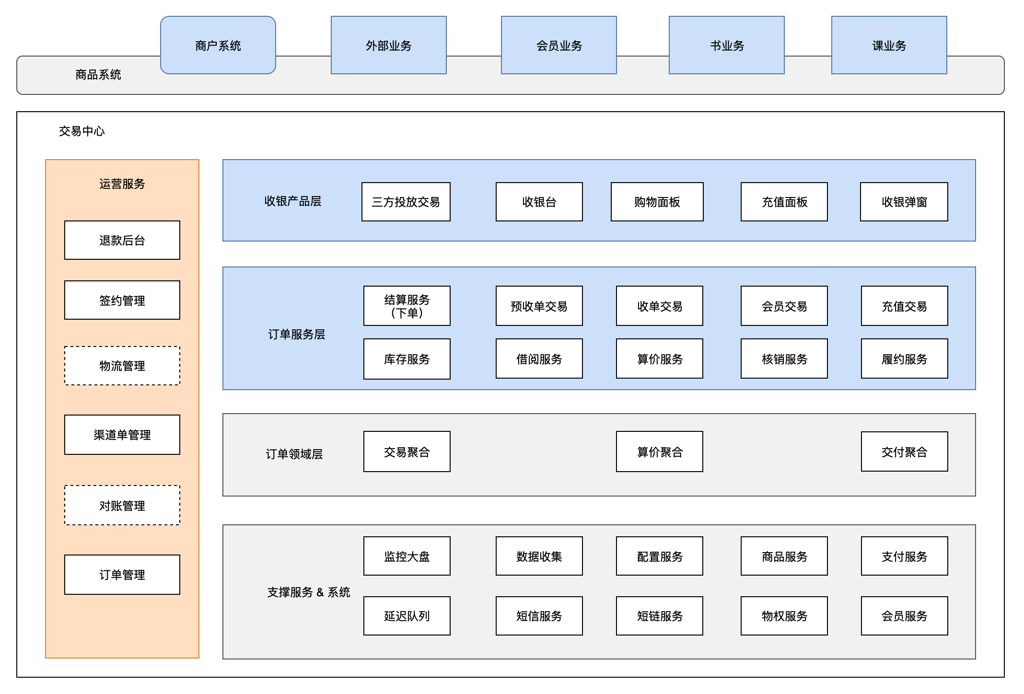
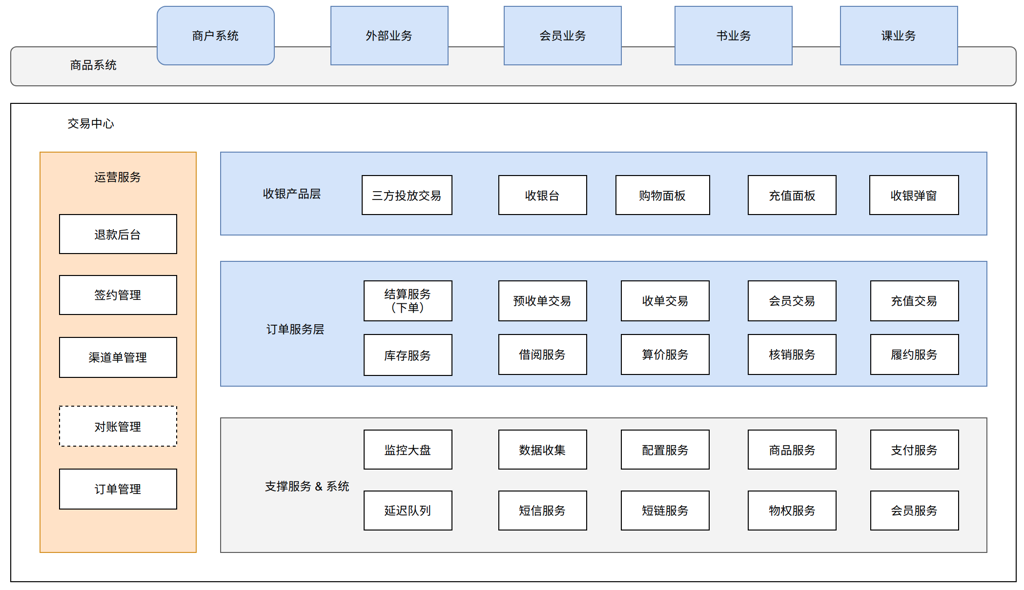
订单系统主要承载知乎站内站外的各种交易服务,提供稳定可靠的交易场景支撑。主要分为以下几个部分:
- 首先产品服务层是面向用户能感受到的交互界面,提供对于这些页面的统一下单支付 API 网关。
- 然后是订单服务层,由上层网关调用,提供着不同场景下的交易服务支撑。
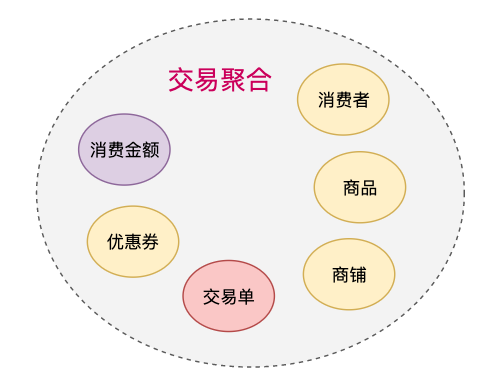
- 再往下是订单领域层,承载订单最核心逻辑代码,首先是用户购买需要的算价聚合,然后是管理订单模型的交易聚合,最后是买完商品后的履约处理的交付聚合。
- 最底层是基础支撑服务层,主要是提供基本的服务支持以及交易依赖的一些服务。
- 最后是运营服务,提供交易相关的后台功能支持。
方法论实践
凡此以上,不论系统迁移方案还是架构理解都归结于参与人员的理解与认知,一个优秀的方案或合适的架构不是设计出来的,是迭代出来的。人的认知也是这样,需要不断的迭代升级,和很多的方法论一样,PDCA 循环为我们提炼了一个提升路径。

- Plan 计划,明确我们迁移的目标,调研现状指定计划。
- Do 执行,实现计划中的内容。
- Check 检查,归纳总结,分析哪些做好了,还有什么问题。
- Action 调整,总结经验教训,在下一个循环中解决。
很多时候,也许你只做了前两步,但其实后两步对你的提升会有很大帮助。所以一个项目的复盘,一次 Code Review 很重要,有语言的交流和碰撞才更容易打破你的固有思维,做到业务认知的提升。
参考文章
https://mp.weixin.qq.com/s/eKc8qoqNCgqrnont2nYNgA
https://zhuanlan.zhihu.com/p/138222300
https://blog.csdn.net/g6U8W7p06dCO99fQ3/article/details/103415254
招聘信息
知乎技术团队大量岗位持续招聘中,欢迎感兴趣的同学加入我们,可投简历至:luohuijuan@zhihu.com